La mesure de la terre (la « géo-métrie », au sens originel) s’est vite imposée aux hommes pour partager un territoire, éviter les conflits, marquer les limites, construire des ponts, préparer la guerre, etc. On sait que les Egyptiens et tous les autres peuples antiques y recouraient et c’est à Thalès, le savant grec (639-548 avant J.-C.) que l’on attribue la technique reposant sur les rapports de distances entre les triangles (d’où le fameux théorème de Thalès, expliqué plus tard par Euclide).

Mais dans la pratique, comment calculer la distance d’un point à un autre ou à un troisième, ou encore la hauteur d’un sommet inaccessible ? Et c’est là qu’interviennent la canne ou le bâton, que l’on dénommait « baculus » chez les Romains. Il est représenté sur plusieurs stèles funéraires exposées au musée du Capitole, à Rome, parmi d’autres instruments de mesure (compas, niveau, équerre). On en trouve des reproductions et beaucoup d’autres informations dans le livre d’Evaristo Luciani : « Histoire des arpenteurs et géomètres des origines à l’an 1900″ (1978). L’une des photos montre notamment le monument funéraire du « mensor » (mesureur) Statilius, orné de cannes pour mesurer et d’un pied du Capitole, divisé en palmes et doigts.
La technique antique fut transmise au fil des siècles et elle était aussi connue des constructeurs médiévaux.

Elle fait l’objet d’exercices chez les scouts et occupe encore une dizaine de pages dans le « Manuel de l’Eclaireur » de 1941. Plusieurs méthodes sont employées, qui reposent toutes sur le calcul des rapports entre les triangles et l’emploi d’un bâton planté dans le sol.

Voici la description de l’une d’elle :
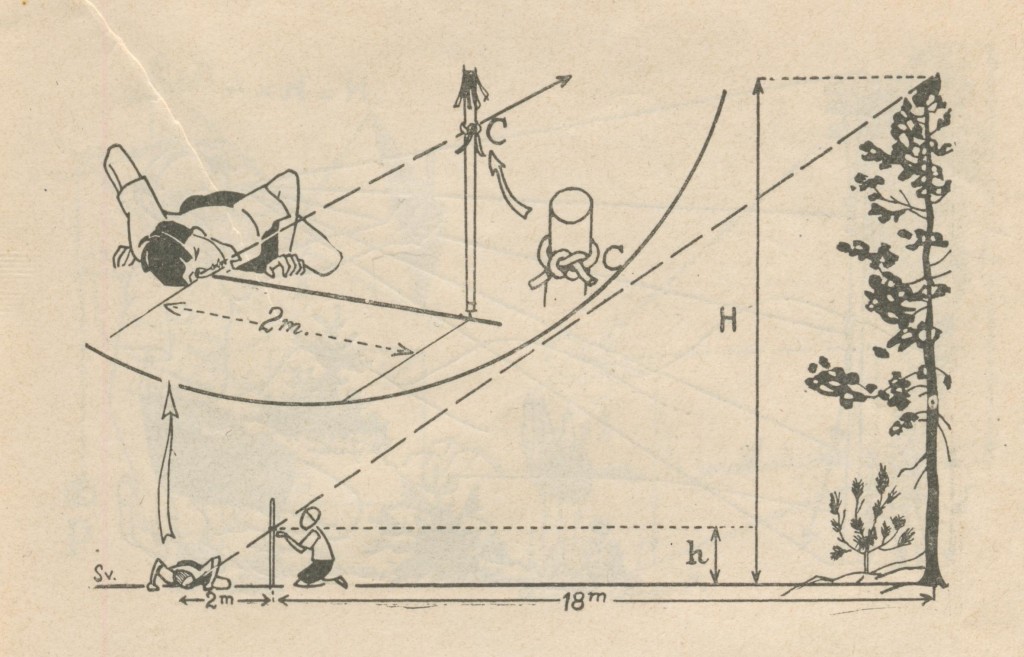
 » Mesurer 18 m, du pied de l’arbre ; planter un bâton ; à 2 m. du bâton, à ras du sol, viser le sommet de l’arbre de façon à pouvoir mesurer la hauteur de la ligne de visée le long du bâton ; 10 fois cette hauteur donnera la hauteur de l’arbre, sans calcul.
La base du grand triangle étant 10 fois plus grande que celle du petit (20 m. et 2 m.). Il est évident que la hauteur à mesurer sera aussi décuple de celle du curseur au-dessus du sol. H = 10 h.

N.B. – Pour gagner du temps, on fera mouvoir le curseur, pendant la visée, par un aide. placer l’oeil qui vise le plus près du sol. »

Article proposé et rédigé par Laurent Bastard. Merci